

The graph below shows point \( P \), the orthogonal. We first discuss what we know about vectors in a 2-dimensional space as used in physics and analytical geometry. A vector space V is a set that is closed under finite vector addition and scalar multiplication operations. This tells you right of the bat that we are not guaranteed that there even exists some sort of.
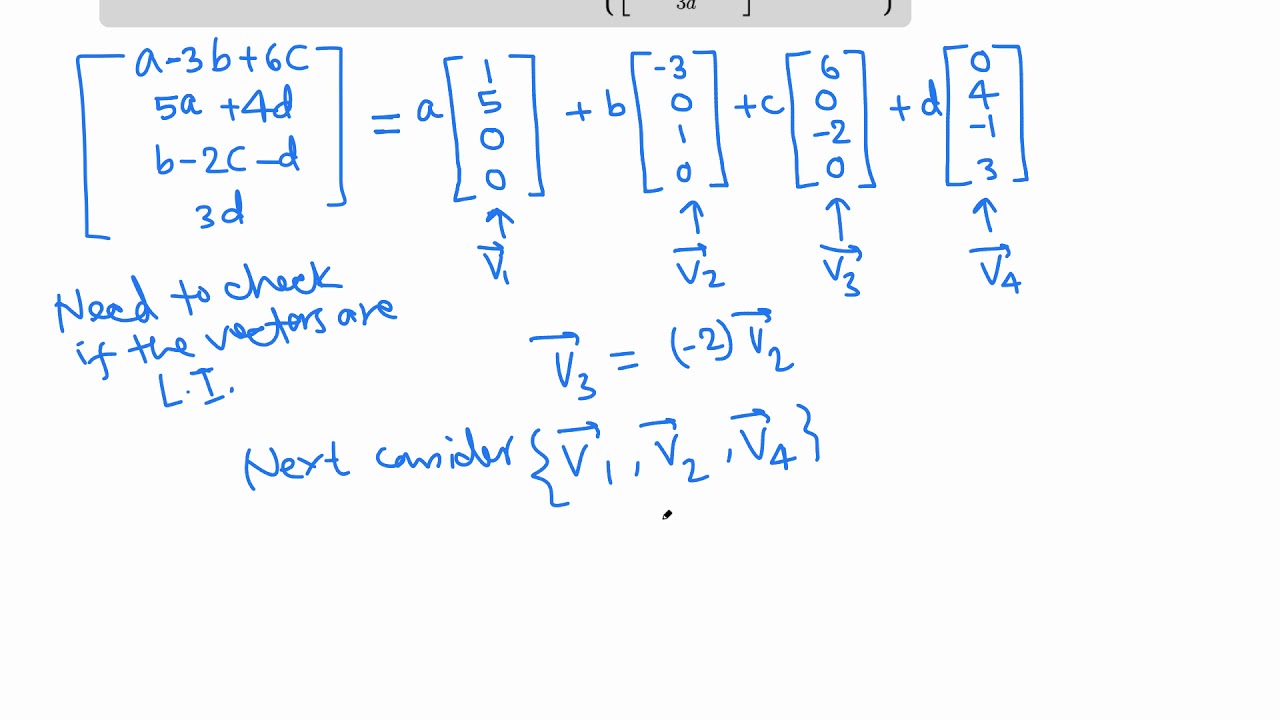
are your operations of vector addition and scalar multiplication (satisfying certain axioms). 2.Basis, Coordinates and Dimension of Vector Spacesīefore we formally define the basis of a vector space, we give examples of basis in two dimensional space which you may already know from physics and/or analytical geometry which may help you understand the concept of basis.ĭefinition of a Basis For 2-Dimensional Space Using Rectangular Axes Recall that a vector space over a field F is defined as a triple ( V, +, ), where V is your set of vectors, and.Remark Suppose that Vis a non-empty subset of Rnthat satisfies properties 2 and 3.

See this theorembelow for a precise statement. If you choose enough vectors, then eventually their span will fill up V,so we already see that a subspace is a span. If in addtition V W, then W is a proper vector subspace of V. In other words, a subspace contains the span of any vectors in it. If W is itself a vector space, then W is said to be a vector subspace of V. Closure under addition: If u and v are in V, then u. 2.2.1 Why define matrix multiplication this way? Definition Let V be a vector space over a field F, and let W be a subset of V. A subspace of R n is a subset V of R n satisfying: Non-emptiness: The zero vector is in V.1.4.3 Transpositions and the sign of a permutation Definition 3.1 Vector Space Axioms Let (K be a field and let) V be a set on which two operations are defined: additions and multiplication by scalars (numbers).1.3.1 Function properties and composition A subset W of a vector space V is called a subspace of V if W is itself a vector space under the addition and scalar multiplication defined on V.1 Sets, functions, relations, permutations.


 0 kommentar(er)
0 kommentar(er)
